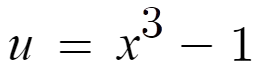Elektronický vzdelávací materiál

Typy funkcií

Prostá funkcia

funkcia f na množine A práve vtedy, keď p∀x1, x2∈A, kde x1≠ x2, sa f(x1) ≠ f(x2)
ak je funkcia rastúca alebo klesajúca je prostá
ak je neklesajúca alebo nerastúca alebo monotónna tak nie je prostá

Párna funkcia

párna je práve vtedy, keď ku každému x∈D(f) existuje -x∈D(f) tak, že f(-x) = f(x)
graf je súmerný podľa súradnicovej osi y

Nepárna funkcia

nepárna je práve vtedy, keď ku každému x∈D(f) existuje -x∈D(f) tak, že f(-x) = -f(x)
graf je súmerný podľa začiatku súradnicovej sústavy

Ohraničená funkcia

ohraničená je práve vtedy, ak je ohraničená zhora aj zdola
zdola platí: ak existuje také číslo d∈R, že pre ∀x∈A je f(x) ≥ d
zhora platí: ak existuje také číslo h∈R, že pre ∀x∈A je f(x) ≤ h

Inverzná funkcia

funkcia f je prostá na celom D(f) a H(f) je jej obor hodnôt, tak sa dá na H(f) definovať funkcia, ktorá každému y∈H(f) priraďuje práve to číslo x∈D(f), pre ktoré sa f(x) = y
pre tieto funkcie platí D(f) = H(f^-1) a H(f) = D(f^-1)
grafy inverznej funkcie sú súmerné podľa priamky p: y = x
inverznú funkciu k funkcii f, označujeme f^-1

Zložená funkcia

funkcia f je zložená, ak ju môžeme zapísať v tvare h(x) = f(g(x)) pre ∀ x∈D(h)
y = f(g(x))
funkciu g(x) = u nazývame vnútorná zložka
funkciu f(u) nazývame vonkajšia zložka zloženej funkcie u
zložená funckia
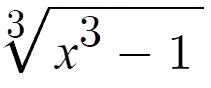
vnútoná zložka
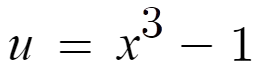
vonkajšia zložka