Mocninová funkcia s prirodzeným exponentom
Mocninová funkcia s prirodzeným exponentom je každá funkcia daná rovnicou: y = xn, kde n ∈ N
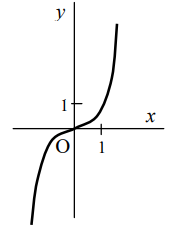
- D(f) = R
- H(f) = R
- je rastúca na celom D(f)
- je nepárna
- nie je ohraničená ani zhora, ani zdola
- nemá ani maximum, ani minimum
- je prostá
Ak n je párne, tak:
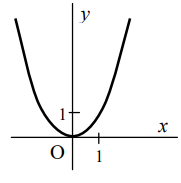
- D(f) = R
- H(f) = (0; ∞)
- je klesajúca na (-∞; 0) a rastúca na(0; ∞)
- je párna
- je zdola ohraničená, zhora nie je ohraničená
- v bode 0 má minimum, maximum nemá
- nie je prostá
Mocninová funkcia s celým exponentom
Mocninová funkcia s celým exponentom je každá funkcia daná rovnicou: y = xm, kde m ∈ Z-
Možno ju zapísať v tvare y = x-n = 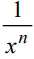 , kde n ∈ N
, kde n ∈ N
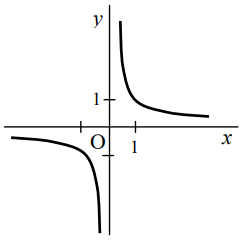
- D(f) = R - {0}
- H(f) = R - {0}
- je klesajúca na celom D(f)
- je nepárna
- nie je ohraničená ani zhora, ani zdola
- nemá ani maximum, ani minimum
- je prostá
Ak n je párne, tak:
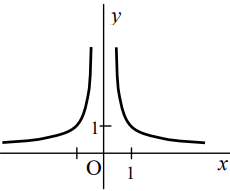
- D(f) = R - {0}
- H(f) = (0;∞)
- je rastúca na (-∞,0) a klesajúca na (0,+∞)
- je párna
- je zdola ohraničená, zhora nie je ohraničená
- nemá ani maximum, ani minimum
- nie je prostá
 Elektronický vzedálací materiál
Elektronický vzedálací materiál 

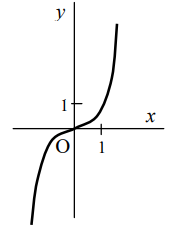
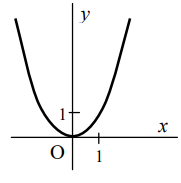
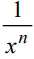 , kde n ∈ N
, kde n ∈ N
