Elektronický vzdelávací materiál

Mnohouholníky

Lomená čiara A₁A₂ ...A _n je zjednotenie úsečiek A₁A₂, A₂A₃, A₃A₄, .... A_{n - 1}A_n Úsečky A₁A₂, A₂A₃, ..., A_{n - 1}A_n, sa nazývajú strany lomenej čiary, body A₁, A₂ ,...,A _n sú vrcholy lomenej čiary.

Lomená čiara sa nazýva jednoduchá, ak:

spoločným bodom každých dvoch strán je vrchol lomenej čiary,

každý vrchol lomenej čiary patrí najviac dvom stranám.

Mnohouholník (n-uholník) A ₁A₂ ...A _n je časť roviny ohraničená jednoduchou uzavretou lomenou čiarou A₁A₂ ...A _n kde n ≥ 3 Body A₁, A₂ ,...,A _n sa nazývajú vrcholy mnohouholníka. Strany lomenej čiary sú strany mnohouholníka.

Strany mnohouholníka, ktoré majú spoločný vrchol, sa nazývajú susedné.

Vrcholy, ktoré ležia na jednej strane lomenej čiary, sa nazývajú susedné.

Uhly určené susednými stranami mnohouholníka, sa nazývajú vnútorné uhly mnohouholníka.

Mnohouholníky sú konvexné aj nekonvexné

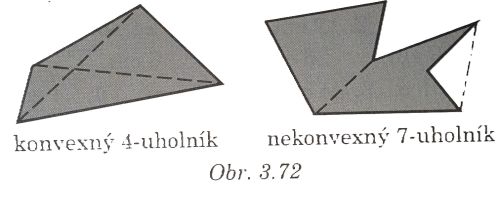
Uhlopriečka mnohouholníka A₁A₂...A_n, je každá úsečka A_iA_j, ktorá nie je strana - je to spojnica nesusedných vrcholov mnohouholníka.

šetky uhlopriečky konvexného mnohouholníka ležia v mnohouholníku.
V nekonvexnom mnohouholníku existuje uhlo-priečka, ktorá v mnohouholníku leží, aj uhlopriečka, ktorá v mnohouholníku neleží.