Elektronický vzdelávací materiál

Valec

Kruhový valec určený kruhom K, bodom A ∈ K a bodom A', ktorý neleží v rovine kruhu K, je množina všetkých bodov všetkých orientovaných úsečiek XX', ktoré majú rovnakú veľkosť a rovnaký smer ako orientovaná úsečka AA', kde X ∈ K.

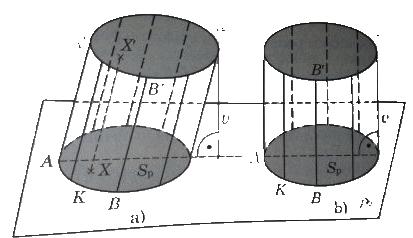
Všetky body X', orientovaných úsečiek XX, kde Xe K, vytvoria kruh K', ktorý je zhodný s kruhom Ka leží v rovine rovnobežnej s rovinou kruhu K. Kruhy K a K'sa nazývajú podstavy kruhového valca.

Úsečky BB', ktoré sú rovnobežné a zhodné s úsečkou AA', pričom bod B leží na hranici kruhu K, sa nazývajú strany valca. Zjednotenie všetkých strán valca je plášť valca.

Valec je rovnostranný, ak je kolmý a platí v = 2*r. Osový rez rovnostranného valca je štvorec.

Pomocou Cavalieriho princípu možno dokázať, že pre objem każ dého valca s obsahom podstavy Sp a výškou v platí:

V = S_p * v = π * r² * v

kde r ∈ R+ je polomer podstavy.
Pre povrch valca platí S = 2 * S_p + Q kde Q je obsah plášťa.
Ak je valec kolmý, tak S = 2πr² + 2πrv = 2πr (r + v)