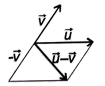Elektronický vzdelávací materiál

Vektory

Čo je to vektor?

Vektor je posunutie.
Usporiadaná dvojica bodov [A, B] je dvojica, v ktorej záleží na poradí.
Bod A je začiatočný bod, bod B je koncový bod úsečky. Nazývame ju aj orientovaná úsečka AB (zápis AB).

Orientovaná úsečka

Nulová orientovaná úsečka AA má začiatočný aj koncový bod v bode A. Veľkosť nulovej orientovanej úsečky je 0.
Veľkosť orientovanej úsečky AB nazývame veľkosť úsečky AB.
Každú orientovanú úsečku AB, ktorá znázorňuje vektor v, budeme nazývať umiestnenie vektora v.
Zápis: v = AB = B - A Na základe tohto môžeme definovať vektor.

Súčet vektorov

u + v je vektor, ktorý vznikne zložením posunutí u, v.
Jeho umiestnením je uhlopriečka rovnobežníka, ktorého strany sú umiestnením vektorov u, v.

Rozdiel vektorov: u - v je vektor u + (- v)

Reálny násobok vektora:

k * u je vektor, ktorého veľkosť je |k|-násobkom veľkosti vektora u, pre k > 0 má smer súhlasne rovnobežný s u, pre
k < 0 má smer nesúhlasne rovnobežný s u.

Pre operácie s vektormi platí:

Veľkosť vektora

Veľkosť vektora u = [u1, u2, u3] v ortonormálnej sústave súradníc je nezáporné reálné číslo |u|= √u1²+u2²+u3²

Uhol vektorov

Ak majú dva nenulové vektory u, v umiestnenia AB, AC, potom konvexný uhol BAC nazývame uhlom vektorov u, v.
Uhol nedefinujeme, ak aspoň jeden z vektorov je nulový.
Pre veľkosť uhla o nenulových vektorov u, v platí:
1. φε 〈0°, 180°〉
2. cos (q = u*v)/(|u|*|v|)

Skalárny súčin vektorov

Ak sú u, v dva nenulové vektory, ktorých uhol má veľkosť q, nazývame číslo |u|*|v|*cos y skalárny súčin vektorov u, v a zapisujeme ho v tvare u*v.

Vlasnosti skalárneho súčinu

Vektorový súčin dvoch vektorov

Vektorovým súčinom vektorov u, v, z ktorých aspoň jeden je nulový, nazývame nulový vektor.
Vlastnosti vektorového súčinu:
Pre každé dva nenulové vektory u, v trojrozmerného priestoru platí:
1. ak v = ku k \in R tak uv = vu = 0
2. uv = - (vu)
Súradnice vektora w ľahko vypočítame podľa nasledujúcej schémy:

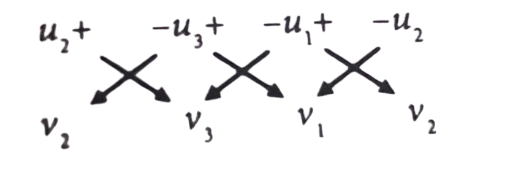
Využitie vektorového súčinu:

Pre obsah rovnobežníka ABCD, kde u = AB, v = AD platí: S = [u x v]
Pre obsah trojuholníka ABC, kde u = AB, v = AC platí: S = 1/2|u x v|
Pre objem rovnobežnostena ABCDEFGH, kde u = AB, v = AD, w = AE platí V = |(u x v) * w|