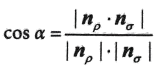Vzdialenosť a odchýlka lineárnych útvarov
Uhol dvoch priamok
- Priamky p, q vytvoria dvojicu vedľajších uhlov. Uhlom priamok nazveme tú z oboch veľkostí, ktorá patrí do intervalu (0°; 90°), označme ho a.
- Veľkosť uhla dvoch priamok v rovine, ale aj v priestore, počítame pomocou ich smerových vektorov.
- Ich uhol môže byť a alebo 180° - a. Platí cos a = cos(180° - a), preto uhol dvoch priamok vypočítame zo vzťahu: cos α=|u*v|/|u|*|v|
- V rovine môžeme použiť namiesto smerových vektorov vektory normálové.
Uhol priamky a roviny.
- Môžeme ho určiť aj pomocou kolmice na rovinu.
- Priamky p a k zvierajú uhol ẞ, priamka p a rovina zvierajú uhol α.
- Platí α = 90° - ẞ, sin α = sin(90° - β) = cos β.
- Uhol dvoch priamok už vieme vypočítať pomocou ich smerových vektorov.
- Smerový vektor kolmice je normálový n.skde vektor roviny.
- Preto uhol priamky a roviny vypočítame: sin α=|n*s|/|n|*|s|, kde n je normálový vektor roviny a s je smerový vektor priamky.
Uhol dvoch rovín.
- Pre každé dve roviny p a σ platí, že ich uhol a sa rovná uhlu dvoch priamok, z ktorých jedna je kolmá na rovinu p a druhú na rovinu σ.
- Priamka kolmá na rovinu má smerový vektor rovný normálovému vektoru roviny.
- Preto môžeme vypočítať uhol dvoch rovín pomocou ich normálových vektorov:
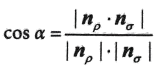
Vzdialenosť bodu od priamky.
- Zápis: |A, p| je vzdialenosť bodu od päty kolmice vedenej daným bodom na danú priamku.
- V rovine: Vzdialenosť bodu A[a1, a2] od priamky p: ax + by + c = 0 vypočítame: |A, p|=(aa₁ + ba₂ + c)/(√a² + b²)
- V priesotre:
- 1. spôsob - smerový vektor priamky je kolmý na vektor AP, kde P je päta kolmice vedenej bodom A na danú priamku => s*AP = 0 a veľkosť vektora AP je vzdialenosť bodu A od priamky p.
- 2. spôsob - Bodom A položíme rovinu α ┴ p, nájdeme p ∩ α = {P}, vzdialenosť bodov A a P je hľadaná vzdialensoť |A, p|
Vzdialenosť bodu od roviny.
- Zápis: |A, p| je vzdialenosť bodu od päty kolmice vedenej daným bodom na danú rovinu.
- Nech bod A[a1, a2, a3] a rovina p: ax + by + cz + d = 0 potom vzdialenosť bodu od roviny vypočítame:|A, p|=
- Preto môžeme vypočítať uhol dvoch rovín pomocou ich normálových vektorov:
- Počítať môžeme aj vzdialenosť dvoch rovnobežných priamok - úlohu prevedieme na vzdialenosť bodu od priamky.
- Vzdialenosť dvoch rovnobežných rovín - úlohu prevedieme na výpočet vzdialenosti bodu od roviny.
- Vzdialenosť priamky rovnobežnej s rovinou - počítame ako vzdialenosť bodu od roviny.
 Elektronický vzedálací materiál
Elektronický vzedálací materiál