Elektronický vzdelávací materiál

Hranol

Hranol určený n-uholníkom A₁ A₂ A₃... An a bodom Ai, ktorý ne- leží v rovine n-uholníka A₁ A₂ A₃... A,, je množina všetkých bodov všetkých orientovaných úsečiek XX', ktoré majú rovnakú veľkosť a rovnaký smer ako orientovaná úsečka A₁A_í, kde X ∈ A₁ A₂ A₃...A_n

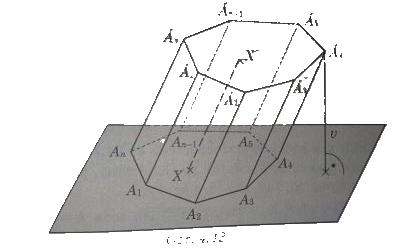
Mnohouholníky A₁ A₂ A₃ ... Á_n a Á₁Á₂Á₃ ... Á_n sú podstavy hranola. Strany oboch podstáv sú podstavné hrany.
Rovnobežníky A₁A₂Á₂Á₁, A₂ A₃ Á₃ Á₂, ..., A_n A₁ Á₁ Á_n sú bočné steny hranola. Úsečky A₁ Á₁, A_n Á_n sú bočné hrany hranola.

Zjednotenie bočných stien hranola je plášť hranola. Zjednotenie plášťa a podstáv je hranica hranola.
Vzdialenosť rovnobežných rovín, v ktorých ležia podstavy hranola, je výška hranola.
Kváder je hranol, ktorého všetky steny sú pravouholníky.
Kocka je hranol, ktorého všetky steny sú štvorce.

Z Cavalieriho princípu vyplýva, že každý hranol s obsahom podstavy S_p, a výškou v má objem:

V = SP*v

Povrch hranola s obsahom podstavy S_p, a obsahom plášťa Q je:

S = 2S_p + Q