Elektronický vzdelávací materiál

Vektor

Orientované úsečky AB a CD sa nazývajú ekvipolentné, ak stred úsečky AD je totožný so stredom úsečky BC, symbolicky.

A + D = B / C

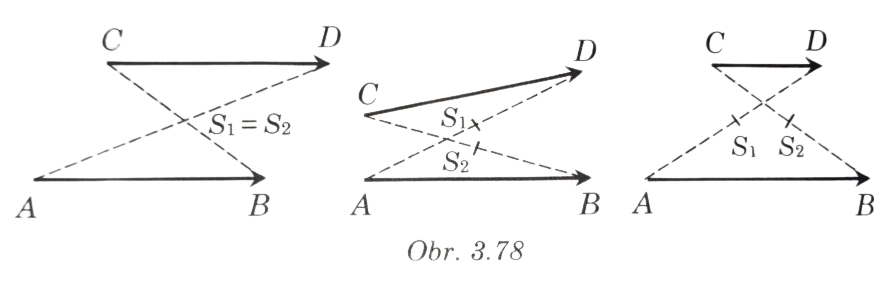
Z obrázka 3.78 vidieť, že orientované úsečky AB a CD sú ekvipolentné, ak majú rovnakú veľkosť a rovnaký smer. Uvažujme orientovanú úsečku AB.

Každý bod roviny môže byť začiatočným bodom orientovanej úsečky, ktorá je ekvipolentná s orientovanou úsečkou AB.

Tak získame nekonečne veľa orientovaných úsečiek, z ktorých každé dve sú ekvipolentné.

Množinu všetkých navzájom ekvipolentných orientovaných úse-čiek nazývame vektor.

vektory budeme v tlačenom texte označovať tučným písmom, napr. a, b, v písanom texte písmenami so šípkou, napr. a, vec b . Teda môžeme napísať napr.

a = {AB, CD, EF ,...,UV,... }

Každú orientovanú úsečku, ktorá patrí vektoru a, nazývame umiestnenie vektora a, píšeme napr.

a = AB ... orientovaná úsečka AB je umiestnením vektora a, resp. vektor a má umiestnenie AB.

Veľkosť vektora a = AB je veľkosť jeho ľubovoľného umiestnenia, teda |a| = |AB|

Množina všetkých nulových orientovaných úsečiek je nulový vektor. Budeme ho označovať o, teda o = {AA, BB, CC ,...} . Jeho veľ-kosť je nula, teda |o| = 0