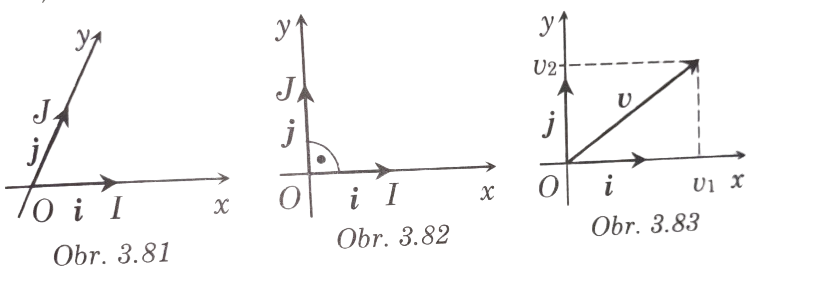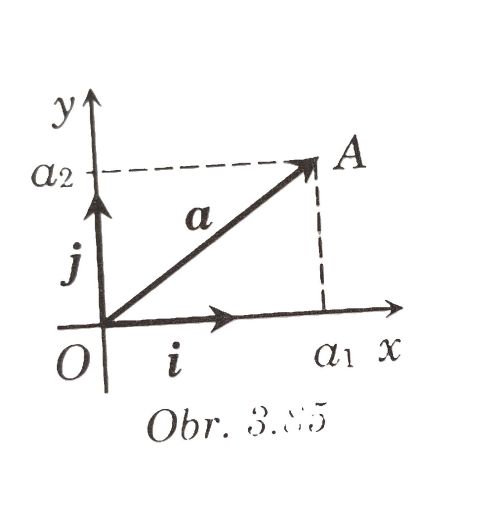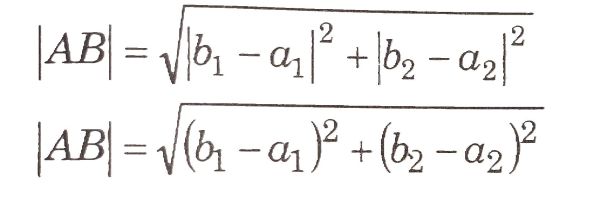Elektronický vzdelávací materiál

Súradnicová sústava v rovine

Súradnicová sústava v rovine je ľubovoľný bod O a dva lineárne nezávislé vektory i = OI j = OJ.

Bod O je začiatok súradnicovej sústavy, priamky x = overline OI y= vec OJ sa nazývajú súradnicové osi.

Označujeme ju (0, x, y) resp. (0, i, j) Ak |i| = |j| = 1 a osi x a y sú kolmé, súradnicová sústava sa nazýva karteziánska.

A. Súradnice vektora

Každý vektor v v rovine je lineárnou kombináciou vektorov i, j, teda existujú reálne čísla v₁,v₂ tak, že v = v₁i + v₂j .

Čísla v₁, v₂ zo vzťahu v = v₁i + v₂j sú súradnice vektora v v súrad nicovej sústave (O, x, y), resp. (O, i, j), teda v = [v₁; v₂] .

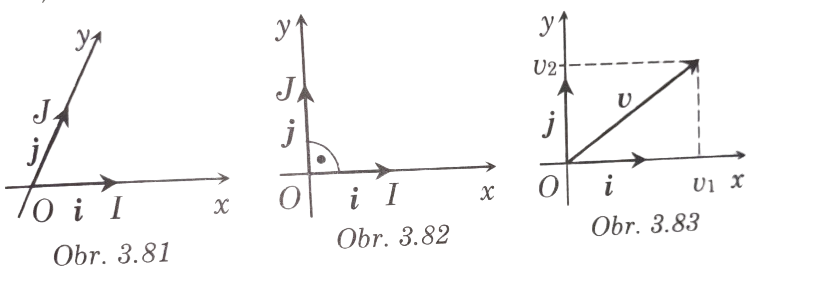
B. Súradnice bodu

Každému bodu A v rovine môžeme priradiť jeho polohový vektor a = OA .

Súradnicami bodu A v (O, x, y) budeme rozumieť súradnice jeho polohového vektora, teda:

A[a₁ ,a ₂ ] ⇔ a = OA = [a₁; a₂]

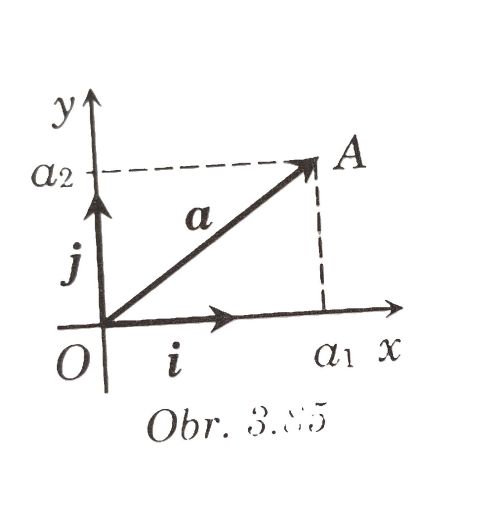
C. Súčet bodu a vektora

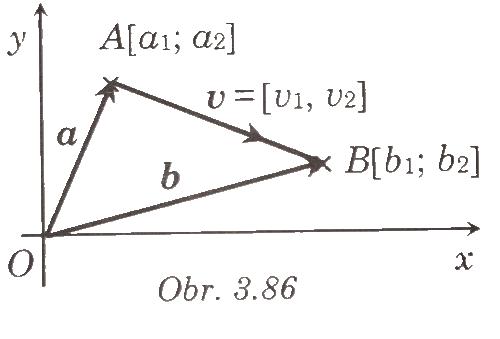
Súčtom bodu A a vektora u nazývame taký bod B, že v = AB Píšeme B = A + v.

Keďže súradnicami bodu B sú súradnice jeho polohového vektora b, platí:

b = a + v = [a₁; a₂] + [v₁; v₂]

b = [a₁+ v₁; a₂ + v₂]

B [a₁ + v₁; a₁ + v₂]

v = b - a = [b₁; b₂] - [a₁; a₂] = [b₁ - a₁; b₂ - a₂]

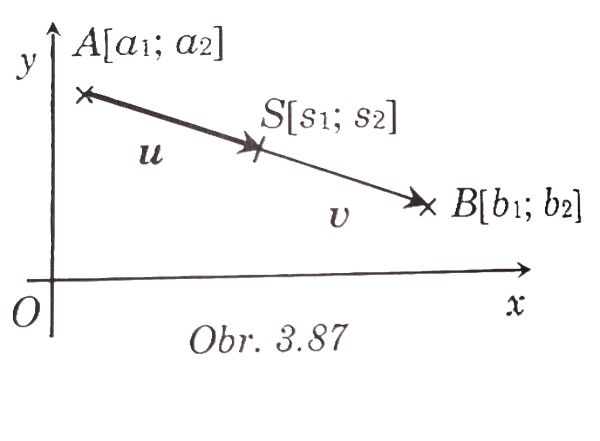
D.Stred úsečky

Uvažujme úsečku AB, kde A[a₁; a₂] B[b₁; b₂] . Nech S[s₁; s₂] je stred úsečky AB.

Zvoľme vektory (obr. 3.87): v = AB = [b₁ - a₁; b₂ - a₂] u = AS = [s₁ - a₁; s₂ - a₂]

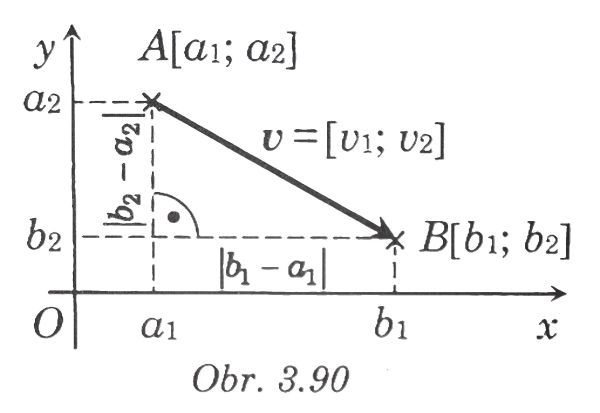
F.Vzdialenosť bodov, velkosť vektora

Vzdialenosť bodov A, B je dĺžka úsečky AB.

Potom pre vzdialenosť bodov A[a₁; a₂] B[b₁; b₂] v karteziánskej súradnicovej sústave (O, x, y) platí:

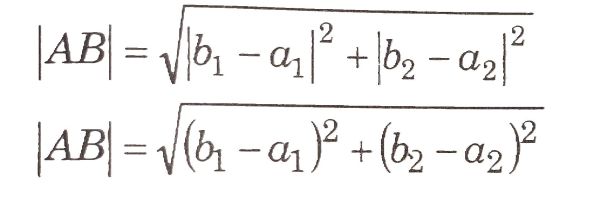
Veľkosť vektora je dĺžka jeho ľubovoľného umiestnenia.

Ak v = AB = B - A , tak v = [b₁ - a₁; b₂ - a₂] = [v₁; v₂]

E. Uhol vektorov

Uhol nenulových vektorov u = AB v = AC konvexný uhol BAC (obr. 3.92). Pre jeho veľkosť φ platí: φ ∈ < 0°, 180° >.

Ak jeden z vektorov u , v je nulový, tak ich uhol nedefinujeme.

Nenulové vektory u , v sa nazývajú kolmé, ak ich umiestnenia ležia na kolmých priamkach, resp. ich uhol má veľkosť 90°,

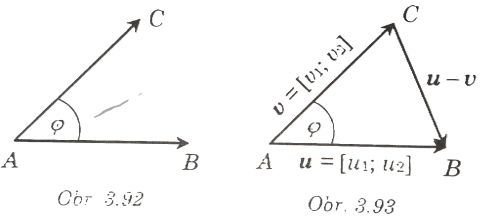
Pre kosinus uhla nenulových vektorov u, ez kosínusovej vety dostaneme :

cos φ =
u₁v₁ + u₂v₂/|u||v|