Elektronický vzdelávací materiál

Telesá

Pojem telesa

Každá množina bodov v priestore je priestorový útvar. Každý pries torový útvar nie je telesom. Telesom rozumieme priestorový útvar, ktorý je ohraničený, uzavretý a súvislý. Čo tieto tri pojmy znamenajú?

Priestorový útvar U je ohraničený, ak existuje také reálne číslo h, že pre každá dva body X, Y ∈ U platí, že XY≤sh.
Priestorový útvar U je súvislý, ak každé dva jeho body možno spojiť krivkou, ktorá loží v útvare U.
Priestorový útvar U je uzavretý, ak obsahuje všetky svoje hra ničné body.

Existuje veľa druhov telies, ale za základné považujeme dva dru by telies: mnohosteny a rotačné telesá.

Mnohosten je teleso, ktorého hranica je zjednotením konečného počtu mnohouholníkov, pričom mnohouholníky, ktoré majú spo ločnú stranu, neležia v jednej rovine
Mnohouholníky, ktoré tvoria hranicu mnohostena, sa nazývajú steny mnohostena. Ich počet označujeme s, v každom mnohostene je s ≥ 4 Vrcholy mnohouholníkov sú vrcholy mnohostena.
Ich počet označujeme v, v každom mnohostene je v ≥ 4 Strany mnohou- holníkov sú hrany mnohostena. Ich počet označujeme h a v každom mnohostene je h ≥ 6

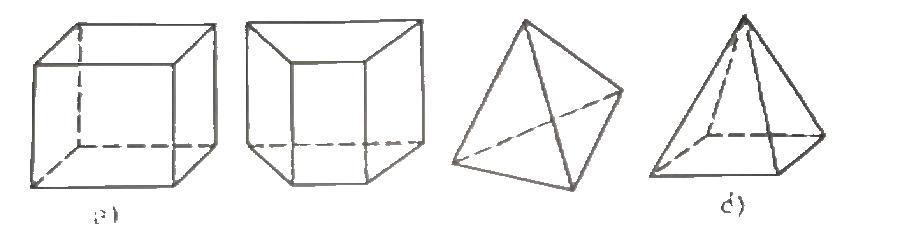
Mnohosten sa nazýva konvexný, ak pre každé dva jeho body X, Y platí, že každý bod úsečky XY je bodom mnohostena. V prvej polovici 18. storočia Leonard Euler dokázal, že pre počet vrcholov, hrán a stien každého konvexného mnohostena platí: v + s = h + 2

Tento poznatok sa nazýva Eulerova veta.

V každom mnohostene je v ≥ 4 s ≥ 4 h ≥ 6 Mnohosten, v ktorom je v = 4 s = 4 h = 6 je najjednoduchší mnohosten. Keďže s = 4, na- zýva sa štvorsten. Hovorí sa mu tiež trojrozmerný simplex (lat. simplex - jednoduchý). Jeho steny sú trojuholníky .

Štvorsten ABCD sa nazýva pravidelný, ak všetky jeho steny sú rovnostranné trojuholníky.

Ťažnica štvorstena je úsečka spájajúca vrchol štvorstena s ťažiskom protiľahlej steny. Ťažnice štvorstena sa pretínajú v jednom bode T' (ťažisku), ktorý delí ťažnice v pomere 3: 1.