Vzájomná poloha dvoch priamok
- Z axióm incidencie vyplýva, že dve rôzne priamky môžu mať spoločný najviac jeden bod.
- Preto ako kritérium na triedenie vzájomných polôh dvoch priamok zvolíme ich prienik.
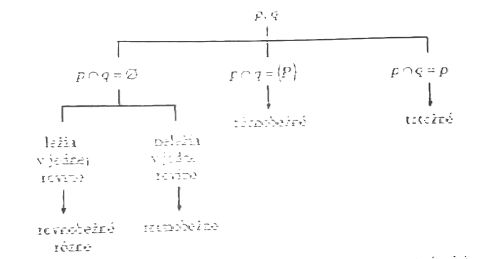
- Priamky p,q sa nazývajú rovnobežné, ak sú totožné alebo p ∩ q = ∅ a ležia v jednej rovine.
- Priamky p, q sa nazývajú rôznobežné, ak p ∩ q = {P}.
- Priamky p, q sa nazývajú mimobežné, ak neležia v jednej rovine.
Vzájomná poloha priamky a rovniny
- Z axióm incidencie vyplýva, že priamka a rovina môžu mať spo- ločný najviac jeden bod alebo celá priamka leží v rovine.
Preto ako kritérium na triedenie vzájomných polôh priamky a roviny zvolíme ich prienik.
Vzájomná poloha dvoch rovín
- Z axióm incidencie vyplýva, že dve rôzne roviny sú disjunktné alebo môžu mať spoločnú priamku.
Preto ako kritérium na triedenie vzájomných polôh dvoch rovín zvolíme ich prienik.
- Roviny σ,σ sa nazývajú rôznobežné, ak ich prienikom je priamka (priesečnica rovín).
- Roviny σ,σ sa nazývajú rovnobežné, ak sú totožné alebo nemajú spoločný bod.
Kritérium rovnobežnosti rovín
- Dve roviny sú rovnobežné, ak jedna z nich obsahuje dve rôznobežné priamky, ktoré sú rovnobežné s druhou rovinou.
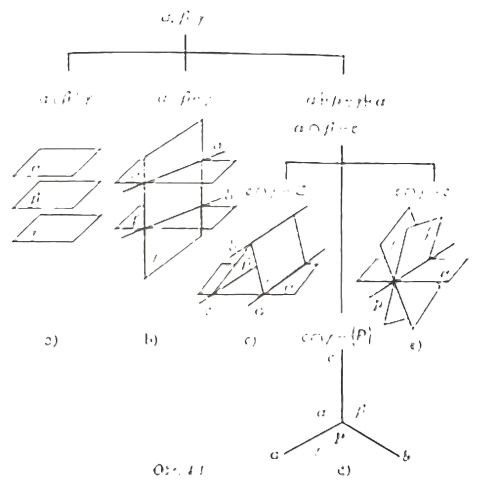
Vzájomná poloha troch rovín
- Kritériom pre triedenie vzájomných polôh troch rovín bude rovnobežnosť rovín.
- Ak dve rovnobežné roviny pretína tretia rovina, tak priesečnice sú rovnobežné
- Ak sú rovnobežné dve z priesečníc troch rovín, pričom každé dve roviny sú rôznobežné, tak je s nimi rovnobežná aj tretia priesečnica
- Ak prechádzajú tým istým bodom dve z priesečníc troch rovín, pričom každé dve roviny sú rôznobežné, tak ním prechádza aj tretia priesečnica
Elektronický vzedálací materiál 